Fork me on GitHub

SSD源码阅读及原理详解

发表于 | 分类于
字数统计: 6,797 | 阅读时长 ≈ 32

  本文阅读的版本是tensorflow对SSD的实现，相对而言阅读难度要远低于caffe版本的实现，源代码可见balancap/SSD-Tensorflow。

一、思路

  SSD的网络结构在论文中清晰可见，如图所示。具体是使用了VGG的基础结构，保留了前五层，将fc6和fc7改为了带孔卷积层，而且去掉了池化层和dropout，在不增加参数的条件下指数级扩大了感受野，而且没有因为池化导致丢失太多的信息；后面再额外增加了3个卷积层和一个average pooling层，目的是使用不同层的feature map来检测不同尺度的物体。之后从前面的卷积层中提取了conv4_3，从后面新增的卷积层中提取了conv7，conv8_2，conv9_2，conv10_2，conv11_2来作为检测使用的特征图，在这些不同尺度特征图上提取不同数目的default boxes，对其进行分类和边框回归得到物体框和类别，最后进行nms来进行筛选。简而言之，SSD预测的目标就是以一张图中的所有提取出的anchor boxes为窗口，检测其中是否有物体，如果有，预测它的类别并对其位置进行精修，没有物体则将其分类为背景。

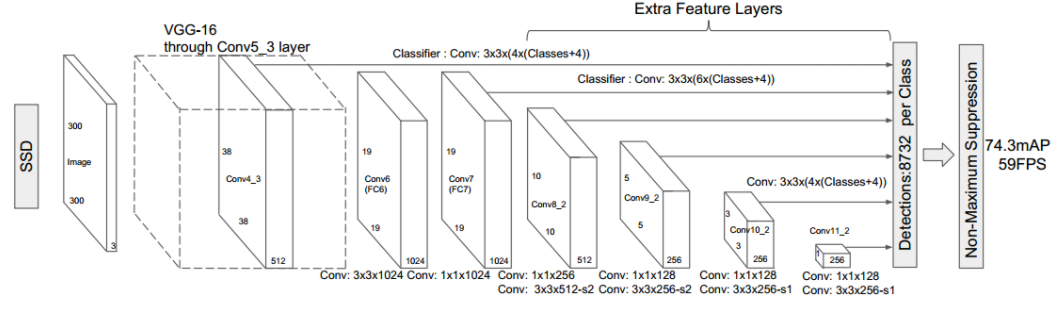
structure.png

  通俗一点的思路如下面的两个图所示，SSD所做的其实就是将feature map用额外的两个卷积层去卷积得到分类评分和边框回归的偏移，其中k表示从该层feature的每个anchor处提取的不同default boxes的个数，这些词具体是什么可以在后面的代码细节中看到。其他的一些细节，例如数据增广，mining hard examples等，也都在代码中有体现。

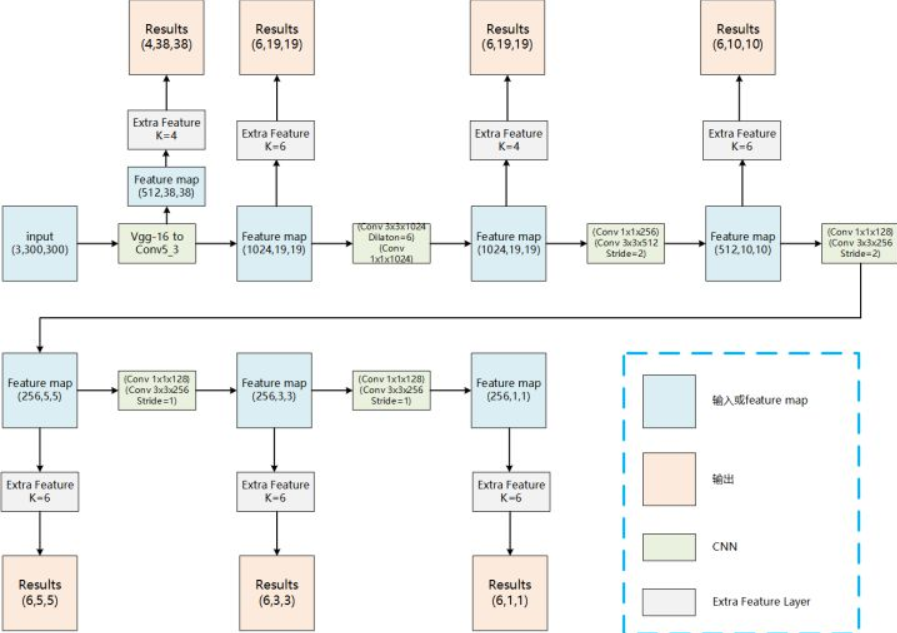
ssdstruct.png

下面是提取结果的卷积层的放大图。

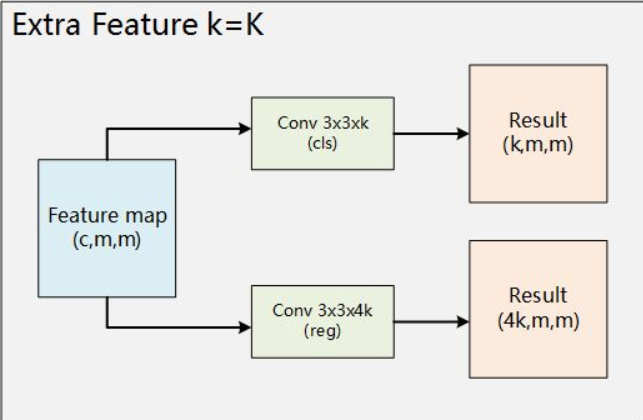
extrafeature.png

  每个feature map可以分两条路，分别得到分类结果和回归结果，再通过已有的ground truth box及其类别得到每个default box的分类和边框偏移，就可以计算loss，进行训练了。

二、default boxes提取

  default boxes的选取与faster rcnn中的anchor有一些类似，就是按照不同的scale和ratio生成k个boxes，看下面的图就能大概了解其思想

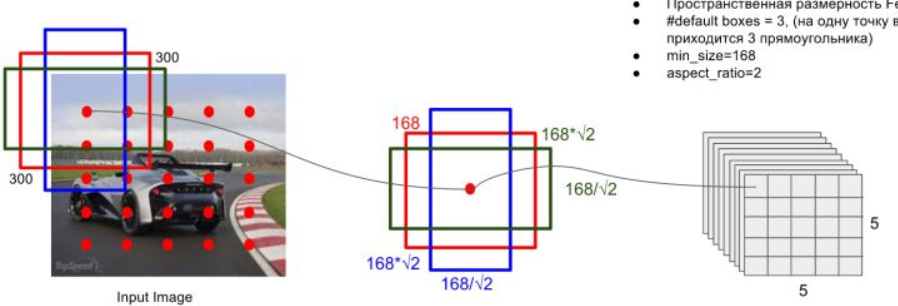
defaultboxes1.png

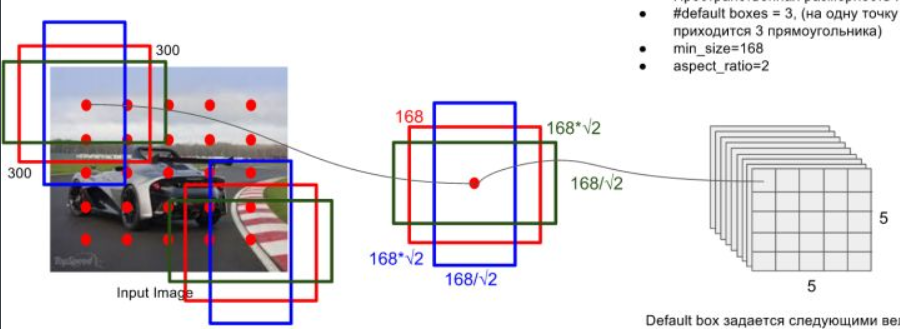
defaultboxes2.png

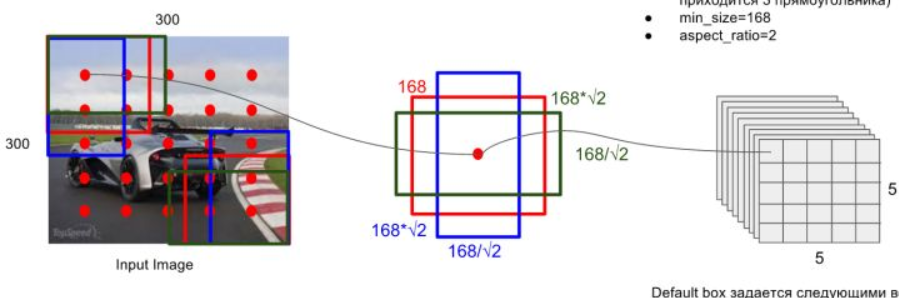
defaultboxes3.png

  • scale：scale指的是所检测的框的大小相对于原图的比例。比例低的可以框出图中的小物体，比例高的可以框出图中的大物体。深层次的feature map适合检测大物体，所以此处使用了一个线性关系来设置各个feature map所检测的scale。公式如下

    其中m是特征图的个数，实际取的时候为5，因为conv4_3层是单独设置的大小。$s_k$是第k个特征图的scale，$s_{min}$和$s_{max}$表示scale的最小值和最大值，在原论文中分别取0.2和0.9，而第一个特征图的scale一般设为$s_{min}$的一半，为0.1，所以对于300$\times$300的图片，最小的比例为300*0.1=30，之后每个对应feature map所检测的default boxes的大小都是300*$s_k$。在caffe源码中的计算是先给出了$s_k$的增长步长，也就是$\displaystyle \lfloor\frac{\lfloor s_{max}\times100\rfloor-\lfloor s_{min}\times100\rfloor}{m-1}\rfloor=17$，由此可以得到5个值分别为20，37，54，71，88（后面还会得到另一个虚拟值是88+17=105）。这些比例乘图片大小再除以100，就能得到各个特征图的大小分别为60，111，162，213，264。再结合最小比例，可以得到default boxes的实际尺度分别为30，60，111，162，213，264。

  • aspect ratio：aspect ratio指的是default boxes的横纵比，一般有$\displaystyle a_r \in \{1,2,3,\frac{1}{2},\frac{1}{3}\}$，对于特定的横纵比，会使用

    来计算真正的宽度和高度（此处$s_k$也是指真实的大小，也就是上文中的30，60，111，…）。默认情况下，每个特征图会有一个$a_r=1$的default box，除此之外还会设置一个$s_k^{\ ‘}=\sqrt{s_k s_{k+1}}$，$a_r=1$的default box，也就是说每个特征图中都会设置两个大小不同的正方形的default box，此处最后一个特征图就需要用到之前的虚拟值105（对应的实际尺度是315）。然而在实现时，使用的比例是可以自己选择的，理论上每个feature map都应该有6个default boxes，但是实际实现中某些层只使用了4个default box，没有使用长宽比为$3$和$\frac{1}{3}$的default box。

  • default box中心：default box的中心在计算的时候需要恢复为原图的相对坐标，所以每个中心设置为$\displaystyle\left(\frac{i+0.5}{|f_k|},\frac{j+0.5}{|f_k|}\right)\ \ i,j \in [0, |f_k|)$，其中$|f_k|$表示第k个feature map的大小。

综上可以得到如下表格

feature map feature map size min_size($\textbf{s}_\textbf{k}$) max_size($\textbf{s}_\textbf{k+1}$) aspect_ratio step
conv4_3 38$\times$38 30 60 1,2,$\frac{1}{2}$ 8
conv7 19$\times$19 60 111 1,2,3,$\frac{1}{2}$,$\frac{1}{3}$ 16
conv8_2 10$\times$10 111 162 1,2,3,$\frac{1}{2}$,$\frac{1}{3}$ 32
conv9_2 5$\times$5 162 213 1,2,3,$\frac{1}{2}$,$\frac{1}{3}$ 64
conv10_2 3$\times$3 213 264 1,2,$\frac{1}{2}$ 100
conv11_2 1$\times$1 264 315 1,2,$\frac{1}{2}$ 300

以上所有的内容在源码中都是有对应的体现的，首先看关于default box的一些设置，代码在ssd_vgg_300.py。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
default_params = SSDParams(
    img_shape=(300, 300),
    num_classes=21,
    no_annotation_label=21,
    feat_layers=['block4', 'block7', 'block8', 'block9', 'block10', 'block11'],
    feat_shapes=[(38, 38), (19, 19), (10, 10), (5, 5), (3, 3), (1, 1)],
    anchor_size_bounds=[0.15, 0.90],
    # anchor_size_bounds=[0.20, 0.90],
    anchor_sizes=[(21., 45.),
                  (45., 99.),
                  (99., 153.),
                  (153., 207.),
                  (207., 261.),
                  (261., 315.)],
    # anchor_sizes=[(30., 60.),
    #               (60., 111.),
    #               (111., 162.),
    #               (162., 213.),
    #               (213., 264.),
    #               (264., 315.)],
    anchor_ratios=[[2, .5],
                   [2, .5, 3, 1./3],
                   [2, .5, 3, 1./3],
                   [2, .5, 3, 1./3],
                   [2, .5],
                   [2, .5]],
    anchor_steps=[8, 16, 32, 64, 100, 300],
    anchor_offset=0.5,
    normalizations=[20, -1, -1, -1, -1, -1],
    prior_scaling=[0.1, 0.1, 0.2, 0.2]
    )

  其中img_shape代表输入图片的大小；num_classes代表输入的类别（20+1个背景类）；feat_layers代表提取的层；feat_shapes代表各个提取的featrue map的大小；anchor_size_bounds代表前文所说的$s_k$（原论文中取0.2到0.9）；anchor_sizes保存的是各层提取的default boxes的大小，也就是上面说的实际尺度；anchor_ratios是前面所说的各层的default boxes的横纵比；anchor_steps指的实际是default box的中心点坐标映射回原图的比例，做法就是用中心点坐标乘以对应的step；anchor_offset对应前文的offset；其余变量暂时与default boxes的生成无关。

  整个训练过程都在train_ssd_network.py中，从这个文件中可以看出，第一步anchors的获取是通过ssd_anchors = ssd_net.anchors(ssd_shape)这句代码来获取的，而ssd_net这个对象是经由一个工厂类生成的一个网络类，此处以ssd_vgg_300为例，可以当作ssd_net就是一个ssd_vgg_300.py中定义的SSDNet的实例。这个被调用的函数可以在ssd_vgg_300.py中找到。而这个函数也只有一句话，那就是

1
2
3
4
5
6
7
return ssd_anchors_all_layers(img_shape,
                              self.params.feat_shapes,
                              self.params.anchor_sizes,
                              self.params.anchor_ratios,
                              self.params.anchor_steps,
                              self.params.anchor_offset,
                              dtype)

ssd_anchors_all_layers在该文件中的后半部分定义，只有几句话：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def ssd_anchors_all_layers(img_shape,
                           layers_shape,
                           anchor_sizes,
                           anchor_ratios,
                           anchor_steps,
                           offset=0.5,
                           dtype=np.float32):
    """Compute anchor boxes for all feature layers.
    """
    layers_anchors = []
    for i, s in enumerate(layers_shape):
        anchor_bboxes = ssd_anchor_one_layer(img_shape, s,
                                             anchor_sizes[i],
                                             anchor_ratios[i],
                                             anchor_steps[i],
                                             offset=offset, dtype=dtype)
        layers_anchors.append(anchor_bboxes)
    return layers_anchors

可以看出，它是一层一层获取default box，再添加到列表中，此处使用了获取一层default box的函数，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def ssd_anchor_one_layer(img_shape,
                         feat_shape,
                         sizes,
                         ratios,
                         step,
                         offset=0.5,
                         dtype=np.float32):
    """Computer SSD default anchor boxes for one feature layer.
    Determine the relative position grid of the centers, and the relative
    width and height.
    Arguments:
      feat_shape: Feature shape, used for computing relative position grids;
      size: Absolute reference sizes;
      ratios: Ratios to use on these features;
      img_shape: Image shape, used for computing height, width relatively to the
        former;
      offset: Grid offset.
    Return:
      y, x, h, w: Relative x and y grids, and height and width.
    """
    # Compute the position grid: simple way.
    # y, x = np.mgrid[0:feat_shape[0], 0:feat_shape[1]]
    # y = (y.astype(dtype) + offset) / feat_shape[0]
    # x = (x.astype(dtype) + offset) / feat_shape[1]
    # Weird SSD-Caffe computation using steps values...
    y, x = np.mgrid[0:feat_shape[0], 0:feat_shape[1]]
    y = (y.astype(dtype) + offset) * step / img_shape[0]
    x = (x.astype(dtype) + offset) * step / img_shape[1]
    # Expand dims to support easy broadcasting.
    y = np.expand_dims(y, axis=-1)
    x = np.expand_dims(x, axis=-1)
    # Compute relative height and width.
    # Tries to follow the original implementation of SSD for the order.
    num_anchors = len(sizes) + len(ratios)
    h = np.zeros((num_anchors, ), dtype=dtype)
    w = np.zeros((num_anchors, ), dtype=dtype)
    # Add first anchor boxes with ratio=1.
    h[0] = sizes[0] / img_shape[0]
    w[0] = sizes[0] / img_shape[1]
    di = 1
    if len(sizes) > 1:
        h[1] = math.sqrt(sizes[0] * sizes[1]) / img_shape[0]
        w[1] = math.sqrt(sizes[0] * sizes[1]) / img_shape[1]
        di += 1
    for i, r in enumerate(ratios):
        h[i+di] = sizes[0] / img_shape[0] / math.sqrt(r)
        w[i+di] = sizes[0] / img_shape[1] * math.sqrt(r)
    return y, x, h, w

代码结合上面的讲解很好理解，通过上述的步骤，就得到了所有层的default box的y，x，h，w。举例来说，对于第一个特征图而言，y，x，h，w，的shape分别为(38,38,1)，(38,38,1)，(4, )，(4, )。

三、Bboxes Encode

  要想理解这部分，需要知道什么是边框回归，此处有一个很好的讲解博客： 边框回归详解 。知道了什么是边框回归，也就能理解我们这一步要干什么，主要有两个任务：1.给每个default box找到其对应的ground truth box，顺带得到其类别和得分。2.计算其相对于对应的ground truth box的变换，也就是边框回归要得到的目标变换。显然，这两步正是相当于给default boxes打上label的过程，对应之前说过的分类任务和回归任务。

  在train的过程中只用一句话得到了每个default box的分类，边框偏移以及得分（用IOU定义，与GT box的IOU越大，得分越高），如下所示：

1
2
gclasses, glocalisations, gscores = \
    ssd_net.bboxes_encode(glabels, gbboxes, ssd_anchors)

这个函数同样在ssd_vgg_300.py，源码是

1
2
3
4
5
6
7
8
9
10
11
def bboxes_encode(self, labels, bboxes, anchors,
                  scope=None):
    """Encode labels and bounding boxes.
    """
    return ssd_common.tf_ssd_bboxes_encode(
        labels, bboxes, anchors,
        self.params.num_classes,
        self.params.no_annotation_label,
        ignore_threshold=0.5,
        prior_scaling=self.params.prior_scaling,
        scope=scope)

可以看出，结果是通过一个叫tf_ssd_bboxes_encode的函数获得的，其定义于ssd_common.py，如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def tf_ssd_bboxes_encode(labels,
                         bboxes,
                         anchors,
                         num_classes,
                         no_annotation_label,
                         ignore_threshold=0.5,
                         prior_scaling=[0.1, 0.1, 0.2, 0.2],
                         dtype=tf.float32,
                         scope='ssd_bboxes_encode'):
    """Encode groundtruth labels and bounding boxes using SSD net anchors.
    Encoding boxes for all feature layers.
    Arguments:
      labels: 1D Tensor(int64) containing groundtruth labels;
      bboxes: Nx4 Tensor(float) with bboxes relative coordinates;
      anchors: List of Numpy array with layer anchors;
      matching_threshold: Threshold for positive match with groundtruth bboxes;
      prior_scaling: Scaling of encoded coordinates.
    Return:
      (target_labels, target_localizations, target_scores):
        Each element is a list of target Tensors.
    """
    with tf.name_scope(scope):
        target_labels = []
        target_localizations = []
        target_scores = []
        for i, anchors_layer in enumerate(anchors):
            with tf.name_scope('bboxes_encode_block_%i' % i):
                t_labels, t_loc, t_scores = \
                    tf_ssd_bboxes_encode_layer(labels, bboxes, anchors_layer,
                                               num_classes, no_annotation_label,
                                               ignore_threshold,
                                               prior_scaling, dtype)
                target_labels.append(t_labels)
                target_localizations.append(t_loc)
                target_scores.append(t_scores)
        return target_labels, target_localizations, target_scores

  可以看出，类似于anchors的获得，default box的标定也是先一个特征图一个特征图进行，之后再将一个特征图的结果分别放入对应列表中。下面来看每个特征图是如何处理的，处理一个特征图的函数是tf_ssd_bboxes_encode_layer，源码见下面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
def tf_ssd_bboxes_encode_layer(labels,
                               bboxes,
                               anchors_layer,
                               num_classes,
                               no_annotation_label,
                               ignore_threshold=0.5,
                               prior_scaling=[0.1, 0.1, 0.2, 0.2],
                               dtype=tf.float32):
    """Encode groundtruth labels and bounding boxes using SSD anchors from
    one layer.
    Arguments:
      labels: 1D Tensor(int64) containing groundtruth labels;
      bboxes: Nx4 Tensor(float) with bboxes relative coordinates;
      anchors_layer: Numpy array with layer anchors;
      matching_threshold: Threshold for positive match with groundtruth bboxes;
      prior_scaling: Scaling of encoded coordinates.
    Return:
      (target_labels, target_localizations, target_scores): Target Tensors.
    """
    # Anchors coordinates and volume.
    yref, xref, href, wref = anchors_layer
    ymin = yref - href / 2.
    xmin = xref - wref / 2.
    ymax = yref + href / 2.
    xmax = xref + wref / 2.
    vol_anchors = (xmax - xmin) * (ymax - ymin)
    # Initialize tensors...
    shape = (yref.shape[0], yref.shape[1], href.size)
    feat_labels = tf.zeros(shape, dtype=tf.int64)
    feat_scores = tf.zeros(shape, dtype=dtype)
    feat_ymin = tf.zeros(shape, dtype=dtype)
    feat_xmin = tf.zeros(shape, dtype=dtype)
    feat_ymax = tf.ones(shape, dtype=dtype)
    feat_xmax = tf.ones(shape, dtype=dtype)
    def jaccard_with_anchors(bbox):
        """Compute jaccard score between a box and the anchors.
        """
        int_ymin = tf.maximum(ymin, bbox[0])
        int_xmin = tf.maximum(xmin, bbox[1])
        int_ymax = tf.minimum(ymax, bbox[2])
        int_xmax = tf.minimum(xmax, bbox[3])
        h = tf.maximum(int_ymax - int_ymin, 0.)
        w = tf.maximum(int_xmax - int_xmin, 0.)
        # Volumes.
        inter_vol = h * w
        union_vol = vol_anchors - inter_vol \
            + (bbox[2] - bbox[0]) * (bbox[3] - bbox[1])
        jaccard = tf.div(inter_vol, union_vol)
        return jaccard
    def intersection_with_anchors(bbox):
        """Compute intersection between score a box and the anchors.
        """
        int_ymin = tf.maximum(ymin, bbox[0])
        int_xmin = tf.maximum(xmin, bbox[1])
        int_ymax = tf.minimum(ymax, bbox[2])
        int_xmax = tf.minimum(xmax, bbox[3])
        h = tf.maximum(int_ymax - int_ymin, 0.)
        w = tf.maximum(int_xmax - int_xmin, 0.)
        inter_vol = h * w
        scores = tf.div(inter_vol, vol_anchors)
        return scores
    def condition(i, feat_labels, feat_scores,
                  feat_ymin, feat_xmin, feat_ymax, feat_xmax):
        """Condition: check label index.
        """
        r = tf.less(i, tf.shape(labels))
        return r[0]
    def body(i, feat_labels, feat_scores,
             feat_ymin, feat_xmin, feat_ymax, feat_xmax):
        """Body: update feature labels, scores and bboxes.
        Follow the original SSD paper for that purpose:
          - assign values when jaccard > 0.5;
          - only update if beat the score of other bboxes.
        """
        # Jaccard score.
        label = labels[i]
        bbox = bboxes[i]
        jaccard = jaccard_with_anchors(bbox)
        # Mask: check threshold + scores + no annotations + num_classes.
        mask = tf.greater(jaccard, feat_scores)
        # mask = tf.logical_and(mask, tf.greater(jaccard, matching_threshold))
        mask = tf.logical_and(mask, feat_scores > -0.5)
        mask = tf.logical_and(mask, label < num_classes)
        imask = tf.cast(mask, tf.int64)
        fmask = tf.cast(mask, dtype)
        # Update values using mask.
        feat_labels = imask * label + (1 - imask) * feat_labels
        feat_scores = tf.where(mask, jaccard, feat_scores)
        feat_ymin = fmask * bbox[0] + (1 - fmask) * feat_ymin
        feat_xmin = fmask * bbox[1] + (1 - fmask) * feat_xmin
        feat_ymax = fmask * bbox[2] + (1 - fmask) * feat_ymax
        feat_xmax = fmask * bbox[3] + (1 - fmask) * feat_xmax
        # Check no annotation label: ignore these anchors...
        # interscts = intersection_with_anchors(bbox)
        # mask = tf.logical_and(interscts > ignore_threshold,
        #                       label == no_annotation_label)
        # # Replace scores by -1.
        # feat_scores = tf.where(mask, -tf.cast(mask, dtype), feat_scores)
        return [i+1, feat_labels, feat_scores,
                feat_ymin, feat_xmin, feat_ymax, feat_xmax]
    # Main loop definition.
    i = 0
    [i, feat_labels, feat_scores,
     feat_ymin, feat_xmin,
     feat_ymax, feat_xmax] = tf.while_loop(condition, body,
                                           [i, feat_labels, feat_scores,
                                            feat_ymin, feat_xmin,
                                            feat_ymax, feat_xmax])
    # Transform to center / size.
    feat_cy = (feat_ymax + feat_ymin) / 2.
    feat_cx = (feat_xmax + feat_xmin) / 2.
    feat_h = feat_ymax - feat_ymin
    feat_w = feat_xmax - feat_xmin
    # Encode features.
    feat_cy = (feat_cy - yref) / href / prior_scaling[0]
    feat_cx = (feat_cx - xref) / wref / prior_scaling[1]
    feat_h = tf.log(feat_h / href) / prior_scaling[2]
    feat_w = tf.log(feat_w / wref) / prior_scaling[3]
    # Use SSD ordering: x / y / w / h instead of ours.
    feat_localizations = tf.stack([feat_cx, feat_cy, feat_w, feat_h], axis=-1)
    return feat_labels, feat_localizations, feat_scores

  这个函数比较长，先看第一个函数之前的部分，首先是通过之前得到的一层特征图的y，x，h，w，计算每个default box的四个角的坐标及面积（此处利用了numpy的广播机制），随后初始化了一些空的tensor：类别标签、得分以及每个default box对应的GT box的四个角的坐标。shape也都符合之前的定义，此处以第一个特征图为例，其大小为38$\times$38，每个中心点对应4个default box，每个default box对应一个label，一个GT box和一个得分，所以所有初始化tensor的shape都是(38,38,4)。

  下面是几个辅助函数，jaccard_with_anchors(bbox)用于计算bbox与所有default box的IOU；intersection_with_anchors(bbox)用于计算bbox与所有default box的交比上default box的面积的值，在此处没有用到这个函数；condition，body要和下面的tf.while_loop连起来看，tf.while_loop的执行逻辑是，若condition为真，执行body，condition只有一句话，其实就是判断i的值是否小于GT box的数目，也就是说整个循环逻辑是以每个GT box为单位进行的，body就是对每个GT box进行的操作。

  在看body具体做了什么之前，需要先了解SSD中GT box的匹配机制。共有两个原则，第一个原则是每个GT box与其IOU最大的defaut box匹配，这样就能保证每个GT box都有一个与其匹配的default box。但是这样的话正负样本严重不平衡，因此还需要第二个原则，那就是对于未匹配的default box，若与某个GT box的IOU大于一个阈值（SSD中取0.5），那么也将其进行匹配，此处有一个问题就是若某个default box与几个GT box的IOU都大于阈值，选哪个与其匹配？显然，选与其IOU最大的那个GT box与之匹配。这样就大大增加了正样本的个数。还会有一个矛盾在于，假如一个GT box 1与其IOU最大的default box小于阈值，而该default box与某一个GT box 2的IOU大于阈值，如何选择。此处应该按照第一个原则，选择GT box 1，因为必须要保证每个GT box要有一个default box与之匹配。（实际情况中该矛盾发生可能较低，所以该tensorflow实现中仅实施了第二个原则。）

  下面可以看一下body函数，可以看出，它的逻辑是使用某个GT box与所有default box的已经匹配的GT box的结果去比较，再决定是否更换每个default box对应的GT box。函数中出现了很多mask*A + (1-mask)*B的模式，mask的值只有0和1两种，那么这句话的意义就很显然了，如果mask为1，新值为A，否则为B，对应到具体情况中就是mask为1则更换对应GT box，为0则保持不变，那么决定是否更换的mask的值则来自于前面的条件判断，条件判断如下

1
2
3
4
5
# Mask: check threshold + scores + no annotations + num_classes.
mask = tf.greater(jaccard, feat_scores)
# mask = tf.logical_and(mask, tf.greater(jaccard, matching_threshold))
mask = tf.logical_and(mask, feat_scores > -0.5)
mask = tf.logical_and(mask, label < num_classes)

  此处更改了之前的逻辑，将大于阈值的部分去掉，改为只要大于之前的IOU，就进行GT box的匹配。

  找到了所有default box对应的GT box的四个角的坐标，就可以开始进行边框偏移的计算，在SSD中此处有一个技巧，假设已知default box的位置$\boldsymbol{d=(d^{cx},d^{cy},d^w,d^h)}$，以及它对应的GT box的位置$\boldsymbol{b=(b^{cx},b^{cy},b^w,b^h)}$，通常的边框偏移是按照如下方式计算的

  这个过程称为编码（encode），对应的解码（decode）过程则为

  但是在SSD中设置了variance来调整对t的放缩，无论在解码还是编码时都会使用variance来控制，此时编码过程计算如下

  解码过程如下

  variance可以选择训练得到还是手动设定，在SSD中选择手动设定，这也就是SSDParams中parior_scaling中四个数的含义，其实就是对应的variance。

四、网络结构

  除了对数据的预处理，以及并行化处理意外，接下来就是将数据喂进网络，得到每个default box的分类结果和边框偏移。接着看train_ssd_network.py，可以看到这样一句代码：

1
2
predictions, localisations, logits, end_points = \
    ssd_net.net(b_image, is_training=True)

  它调用了net函数，返回了四个变量，为了清楚这个函数做了什么，提前说明四个变量的含义：predictions就是default box在各个类上的得分，也就是后面的logits通过softmax得到的结果，这样logits是什么就无需解释了，localisations是对default box的边框偏移预测结果，end_points是一个字典，里面储存着各个block的输出特征图。

  下面来看net函数，发现它的核心只有一句话

1
2
3
4
5
6
7
8
9
10
11
r = ssd_net(inputs,
            num_classes=self.params.num_classes,
            feat_layers=self.params.feat_layers,
            anchor_sizes=self.params.anchor_sizes,
            anchor_ratios=self.params.anchor_ratios,
            normalizations=self.params.normalizations,
            is_training=is_training,
            dropout_keep_prob=dropout_keep_prob,
            prediction_fn=prediction_fn,
            reuse=reuse,
            scope=scope)

  而ssd_net是定义在跟net相同文件（ssd_vgg_300.py）中的一个函数，我们可以在下面找到它的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
def ssd_net(inputs,
            num_classes=SSDNet.default_params.num_classes,
            feat_layers=SSDNet.default_params.feat_layers,
            anchor_sizes=SSDNet.default_params.anchor_sizes,
            anchor_ratios=SSDNet.default_params.anchor_ratios,
            normalizations=SSDNet.default_params.normalizations,
            is_training=True,
            dropout_keep_prob=0.5,
            prediction_fn=slim.softmax,
            reuse=None,
            scope='ssd_300_vgg'):
    """SSD net definition.
    """
    # if data_format == 'NCHW':
    #     inputs = tf.transpose(inputs, perm=(0, 3, 1, 2))
    # End_points collect relevant activations for external use.
    end_points = {}
    with tf.variable_scope(scope, 'ssd_300_vgg', [inputs], reuse=reuse):
        # Original VGG-16 blocks.
        net = slim.repeat(inputs, 2, slim.conv2d, 64, [3, 3], scope='conv1')
        end_points['block1'] = net
        net = slim.max_pool2d(net, [2, 2], scope='pool1')
        # Block 2.
        net = slim.repeat(net, 2, slim.conv2d, 128, [3, 3], scope='conv2')
        end_points['block2'] = net
        net = slim.max_pool2d(net, [2, 2], scope='pool2')
        # Block 3.
        net = slim.repeat(net, 3, slim.conv2d, 256, [3, 3], scope='conv3')
        end_points['block3'] = net
        net = slim.max_pool2d(net, [2, 2], scope='pool3')
        # Block 4.
        net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='conv4')
        end_points['block4'] = net
        net = slim.max_pool2d(net, [2, 2], scope='pool4')
        # Block 5.
        net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='conv5')
        end_points['block5'] = net
        net = slim.max_pool2d(net, [3, 3], stride=1, scope='pool5')
        # Additional SSD blocks.
        # Block 6: let's dilate the hell out of it!
        net = slim.conv2d(net, 1024, [3, 3], rate=6, scope='conv6')
        end_points['block6'] = net
        net = tf.layers.dropout(net, rate=dropout_keep_prob, training=is_training)
        # Block 7: 1x1 conv. Because the fuck.
        net = slim.conv2d(net, 1024, [1, 1], scope='conv7')
        end_points['block7'] = net
        net = tf.layers.dropout(net, rate=dropout_keep_prob, training=is_training)
        # Block 8/9/10/11: 1x1 and 3x3 convolutions stride 2 (except lasts).
        end_point = 'block8'
        with tf.variable_scope(end_point):
            net = slim.conv2d(net, 256, [1, 1], scope='conv1x1')
            net = custom_layers.pad2d(net, pad=(1, 1))
            net = slim.conv2d(net, 512, [3, 3], stride=2, scope='conv3x3', padding='VALID')
        end_points[end_point] = net
        end_point = 'block9'
        with tf.variable_scope(end_point):
            net = slim.conv2d(net, 128, [1, 1], scope='conv1x1')
            net = custom_layers.pad2d(net, pad=(1, 1))
            net = slim.conv2d(net, 256, [3, 3], stride=2, scope='conv3x3', padding='VALID')
        end_points[end_point] = net
        end_point = 'block10'
        with tf.variable_scope(end_point):
            net = slim.conv2d(net, 128, [1, 1], scope='conv1x1')
            net = slim.conv2d(net, 256, [3, 3], scope='conv3x3', padding='VALID')
        end_points[end_point] = net
        end_point = 'block11'
        with tf.variable_scope(end_point):
            net = slim.conv2d(net, 128, [1, 1], scope='conv1x1')
            net = slim.conv2d(net, 256, [3, 3], scope='conv3x3', padding='VALID')
        end_points[end_point] = net
        # Prediction and localisations layers.
        predictions = []
        logits = []
        localisations = []
        for i, layer in enumerate(feat_layers):
            with tf.variable_scope(layer + '_box'):
                p, l = ssd_multibox_layer(end_points[layer],
                                          num_classes,
                                          anchor_sizes[i],
                                          anchor_ratios[i],
                                          normalizations[i])
            predictions.append(prediction_fn(p))
            logits.append(p)
            localisations.append(l)
        return predictions, localisations, logits, end_points

  代码结构十分清晰，首先看前面定义网络的部分，这个定网络的定义与VGG16类似，只不过替换了其中某些层，原因在第一部分可以看到，可以看到在这一部分中每个block的输出被放进了end_points字典中。而后面则是根据特征图生成分类结果和偏移结果的部分，可以看到也是逐层进行并放到一个列表中的形式，每一层预测结果的获得都调用了ssd_multibox_layer函数，下面就看一下该函数的内容。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def ssd_multibox_layer(inputs,
                       num_classes,
                       sizes,
                       ratios=[1],
                       normalization=-1,
                       bn_normalization=False):
    """Construct a multibox layer, return a class and localization predictions.
    """
    net = inputs
    if normalization > 0:
        net = custom_layers.l2_normalization(net, scaling=True)
    # Number of anchors.
    num_anchors = len(sizes) + len(ratios)
    # Location.
    num_loc_pred = num_anchors * 4
    loc_pred = slim.conv2d(net, num_loc_pred, [3, 3], activation_fn=None,
                           scope='conv_loc')
    loc_pred = custom_layers.channel_to_last(loc_pred)
    loc_pred = tf.reshape(loc_pred,
                          tensor_shape(loc_pred, 4)[:-1]+[num_anchors, 4])
    # Class prediction.
    num_cls_pred = num_anchors * num_classes
    cls_pred = slim.conv2d(net, num_cls_pred, [3, 3], activation_fn=None,
                           scope='conv_cls')
    cls_pred = custom_layers.channel_to_last(cls_pred)
    cls_pred = tf.reshape(cls_pred,
                          tensor_shape(cls_pred, 4)[:-1]+[num_anchors, num_classes])
    return cls_pred, loc_pred

  ssd_multibox_layer同样定义于ssd_vgg_300.py中，可以看到一开始对normalization值进行了判断，此处就是SSDParams中normalizations的作用，在SSD中由于第一个要提取特征层较浅，其norm较大，所以要对其进行沿channel方向的l2_normalize，而其他层无需进行此操作，代码中也仅是判断了normalization的值是否大于0，所以在normalizations中第一个值大于0，其他都小于0，20和-1无实际含义。

  下面则是对location的计算，首先使用了一个3*3卷积，通道数是每个中心default box的个数乘4，代表y，x，w，h四个偏移，从而得到了每个中心的边框偏移的结果，此处又进行了一个reshape操作，其中tensor_shape得到loc_pred的形状，再通过切片将最后一维去掉，再加上两维，分别是每个中心default box的个数，和4，这样就得到了[batch_size,size[0],size[1],num_anchors,4]的tensor。以第二个特征层为例，loc_pred的形状为[batch_size,19,19,6,4]，同理可以得到第二个特征层的cls_pred的形状为[batch_size,19,19,6,21]。

五、loss的计算

  SSD的loss是一个multitask的loss，包含分类损失和定位损失，公式如下所示

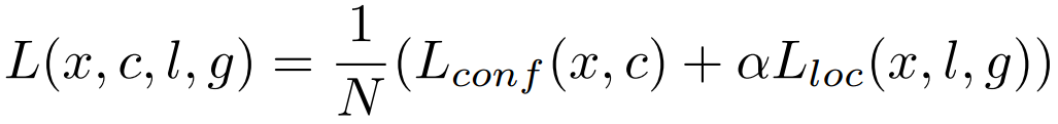
total_loss.png

  所有此处所有的loss值均是对一张图而言的，式子中的$N$代表所有default box中正样本（有对应GT box）的数量，$\alpha$用于调整分类损失和定位损失的比例，下面看一下二者的具体计算。

  首先看分类损失

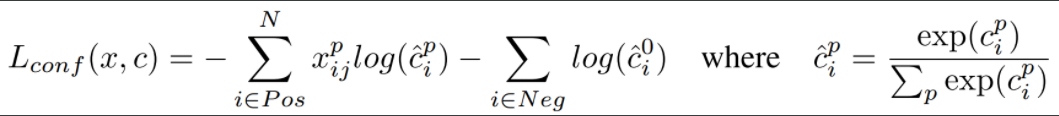
conf_loss.png

  式子中的$x_{ij}^p\in \{0,1\}$，类似于一个指示函数，当第i个default box与第j个GT box匹配并属于第p类时，$x_{ij}^p=1$，其他情况下$x_{ij}^p=0$。显然$c_i^p$就是之前得到的logits，所以整个式子其实就是一个交叉熵损失。

​ 接下来看一下定位损失。

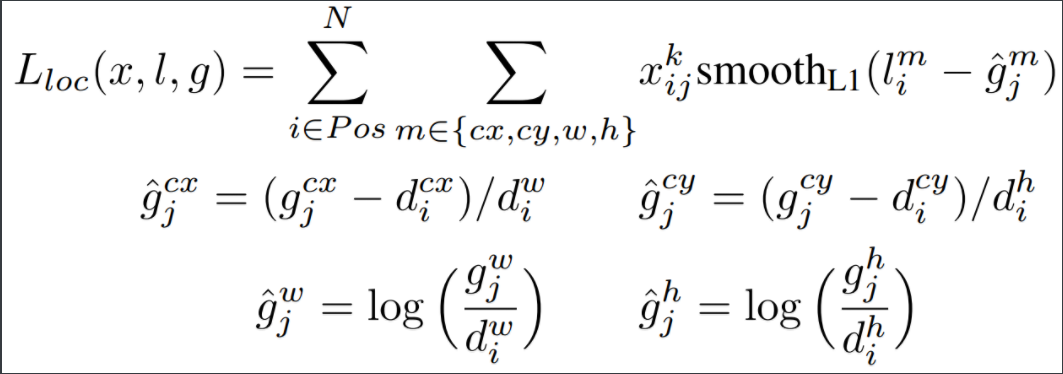
loc_loss.png

  定位损失中的$x_{ij}^p$与分类损失中的含义相同，$\hat g_j^m$根据下面的定义，含义是default box到其对应GT box的偏移，$l_i^m$则是预测的偏移，对二者的误差使用了smooth L1 loss。

  与之前的过程类似，可以在train_ssd_network.py中看到求loss的代码，如下

1
2
3
4
5
6
ssd_net.losses(logits, localisations,
               b_gclasses, b_glocalisations, b_gscores,
               match_threshold=FLAGS.match_threshold,
               negative_ratio=FLAGS.negative_ratio,
               alpha=FLAGS.loss_alpha,
               label_smoothing=FLAGS.label_smoothing)

  它调用了SSDNet的losses函数，只有一句话

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def losses(self, logits, localisations,
           gclasses, glocalisations, gscores,
           match_threshold=0.5,
           negative_ratio=3.,
           alpha=1.,
           label_smoothing=0.,
           scope='ssd_losses'):
    """Define the SSD network losses.
    """
    return ssd_losses(logits, localisations,
                      gclasses, glocalisations, gscores,
                      match_threshold=match_threshold,
                      negative_ratio=negative_ratio,
                      alpha=alpha,
                      label_smoothing=label_smoothing,
                      scope=scope)

  它调用的ssd_losses是定义在相同文件中的函数，为了减少说明，使用了网上的有注释的版本，如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
# =========================================================================== #
# SSD loss function.
# =========================================================================== #
#logits.shape=[(5,38,38,4,21),(5,19,19,6,21),(5,10,10,6,21),(5,5,5,6,21),(5,3,3,4,21),(5,1,1,4,21)]
#localisations.shape=[(5,38,38,4,4),(5,19,19,6,4),(5,10,10,6,4),(5,5,5,6,4),(5,3,3,4,4),(5,1,1,4,4)],glocalisations同
#gclasses.shape=[(5,38,38,4),.................], gscores同
def ssd_losses(logits, localisations,             
               #预测类别, 预测位置
               gclasses, glocalisations, gscores,
               #ground truth 类别, ground truth 位置, ground truth 分数
               match_threshold=0.5,
               negative_ratio=3.,
               alpha=1.,
               label_smoothing=0.,
               device='/cpu:0',
               scope=None):
    with tf.name_scope(scope, 'ssd_losses'):
        lshape = tfe.get_shape(logits[0], 5)
        num_classes = lshape[-1]
        batch_size = lshape[0]	#5
 
        # Flatten out all vectors!
        flogits = []
        fgclasses = []
        fgscores = []
        flocalisations = []
        fglocalisations = []
        for i in range(len(logits)):
            flogits.append(tf.reshape(logits[i], [-1, num_classes]))
            fgclasses.append(tf.reshape(gclasses[i], [-1]))
            fgscores.append(tf.reshape(gscores[i], [-1]))
            flocalisations.append(tf.reshape(localisations[i], [-1, 4]))
            fglocalisations.append(tf.reshape(glocalisations[i], [-1, 4]))
 
        #flogits.shape=[shape=(5×38×38×4,21), shape=(5×19×19×6,21), ......], 共6个feature map的组成
        #fgclasses.shape=[shape=(5×38×38×4), shape=(5×19×19×6), ......]其它相似
 
        # And concat the crap!
        #logits.shape=(5×38×38×4+5×19×19×6+...+5×1×1×4, 21)
        #将[flogits[1],flogits[2],...,flogits[i],...]按第一维组合在一起，下同
        logits = tf.concat(flogits, axis=0) 
        
        gclasses = tf.concat(fgclasses, axis=0)
        gscores = tf.concat(fgscores, axis=0)
        localisations = tf.concat(flocalisations, axis=0)
        glocalisations = tf.concat(fglocalisations, axis=0)
        dtype = logits.dtype
 
        # Compute positive matching mask...
        pmask = gscores > match_threshold   #得分>0.5的为正样本(掩码)
        fpmask = tf.cast(pmask, dtype)
        n_positives = tf.reduce_sum(fpmask) #正样本数
 
        # Hard negative mining...
        no_classes = tf.cast(pmask, tf.int32)
        predictions = slim.softmax(logits)
        nmask = tf.logical_and(tf.logical_not(pmask), #得分>-0.5且<=0.5的样本
                               gscores > -0.5)
        fnmask = tf.cast(nmask, dtype) 
        
        #得分>-0.5且<=0.5的样本在第0类（负样本）处的预测值（softmax）. 
        #nvalues=[[p1],[p2],...,[pN]],N为一个batch中的anchors的总数,
        #满足score>0.5的样本,pi=0
        nvalues = tf.where(nmask,                     
                           predictions[:, 0],
                           1. - fnmask)
                           
        #nvalues_flat=[p1,p2,...,pN]
        nvalues_flat = tf.reshape(nvalues, [-1])
        
        # Number of negative entries to select.
        #负样本数取满足-0.5<score<=0.5和3倍正样本数中的最小值（保证正负样本比例不小于1:3）
        max_neg_entries = tf.cast(tf.reduce_sum(fnmask), tf.int32)
        n_neg = tf.cast(negative_ratio * n_positives, tf.int32) + batch_size
        n_neg = tf.minimum(n_neg, max_neg_entries)
 
        #返回-nvalues_flat中最大的k(n_neg)值,和其索引(从0开始),即nvalues_flat中最小的k个值
        val, idxes = tf.nn.top_k(-nvalues_flat, k=n_neg)
        #nvalues_flat中最小的k个值中的最大值,对应样本记为Max Negative Hard样本
        max_hard_pred = -val[-1]
        # Final negative mask.
        #最终负样本为置信度小于Max Negative Hard的所有样本
        nmask = tf.logical_and(nmask, nvalues < max_hard_pred)
        fnmask = tf.cast(nmask, dtype)
 
        # Add cross-entropy loss.
        with tf.name_scope('cross_entropy_pos'):
            loss = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits,
                                                                  labels=gclasses)
            
            #loss乘正样本掩码得符合条件的正样本损失；损失除以batch_size(这里为5)
            loss = tf.div(tf.reduce_sum(loss * fpmask), batch_size, name='value') 
            tf.losses.add_loss(loss)		#将当前loss添加到总loss集合
 
        with tf.name_scope('cross_entropy_neg'):
            loss = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits,
                                                                  labels=no_classes)
            loss = tf.div(tf.reduce_sum(loss * fnmask), batch_size, name='value')
            tf.losses.add_loss(loss)		#将当前loss添加到总loss集合
 
        # Add localization loss: smooth L1, L2, ...
        with tf.name_scope('localization'):
            # Weights Tensor: positive mask + random negative.
            weights = tf.expand_dims(alpha * fpmask, axis=-1) #位置项损失权重α
            loss = custom_layers.abs_smooth(localisations - glocalisations)
            loss = tf.div(tf.reduce_sum(loss * weights), batch_size, name='value')
            
            #将当前loss添加到总loss集合，最后通过tf.losses.get_total_loss()计算所有的loss
            tf.losses.add_loss(loss)

六、Data Augmentation

  此处数据增强在tf中有很多辅助函数，而pytorch对ssd的实现中（amdegroot/ssd.pytorch）数据增强的部分都是使用的自己写的函数，先读HSV颜色空间相关内容，占坑。