word2vec理解

  本文需要对n-gram模型在评估语句上的应用有一定了解（n-gram还有一些其他应用，如模糊匹配、特征工程等），可以看作对word2vec 中的数学原理详解这篇博文的一些思考。

  首先一定要建立起word2vec的基本认识，在NLP的一些任务中，我们需要将自然语言进行处理并发现其中的规律。但是机器没有办法直接理解自然语言，这就需要我们将其抽象化，换成一种机器能理解的表示方式。这就是word2vec的目的，将训练集中的词语表示成n维向量空间中的一个向量，而这个向量要对解决的问题有着尽可能好的特征表示。由此可以看出，word2vec与要解决的问题（也就是要训练的语言模型）是紧密相关的，所以一般情况下他们是一起进行训练的。例如keras中的Embedding层，官方解释是将字典下标转换为固定大小的向量。事实上这就是word2vec的一个过程，暂且不提keras是如何做的，要明确的一点是，Embedding层中的参数也是要随着训练的模型一起更新的，这有助于更好地理解之后的Skip-gram和CBOW模型。

神经网络语言模型

  先看一下通用的语言模型，如下图所示。下面对这个图做出一些解释，这是一个三层语言模型，首先看输入，$w_{t-n+1},\dots,w_{t-2}, w_{t-1}$等是$w_t$之前的n-1个词，index的含义是他们在词典中的下标；再看输出，第i个输出是$P(w_t=i|context)$，其中context表示$w_t$的上下文，在这里表示输入的之前的n-1个词。所以这个模型就是计算了已知前n-1个词，而第n个词为i的条件概率。按照论文中的解释，这个网络有三层，如下：

• 输入层（Input Layer）：负责将词向量输入，也就是$C(w_{t-n+1}),\dots,C(w_{t-2}),C(w_{t-1})$，每个用m维向量表示，共n-1个首尾相接，所以形成了一个m(n-1)维的向量。

• 隐含层（Hidden Layer）：设之前得到的m(n-1)维的向量为X，则隐含层的输出$Z = tanh(WX + p)$。其中W为该层权重，也就是要训练的参数，p是bias。输出使用tanh作为activation function，所以不用做smoothing。

• 输出层（Outpu Layer）：输出层的结点数与词典的大小相同，代表下一个词是词典中某一个词的概率。按照图中所说就是$O = softmax(UZ + q)$。其中U为该层权重，q是bias，softmax是activation function。

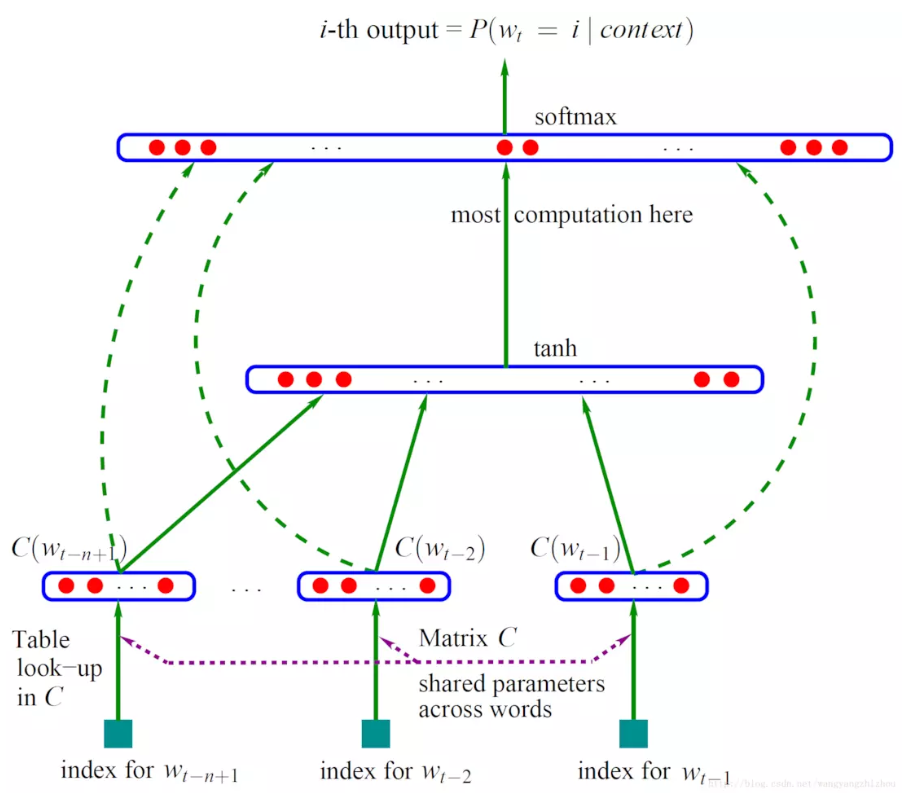
  之后要介绍的网络都建立在这个三层模型的基础上，只是对一些流程做出了改动。

CBOW

  这个模型要解决的问题其实就是在知道当前词$w_t$的上下文$w_{t-2},w_{t-1},w_{t+1},w_{t+2}$的情况下，预测$w_t$。也就是要计算$P(w_t|context(w_t))$。大体如下图所示：

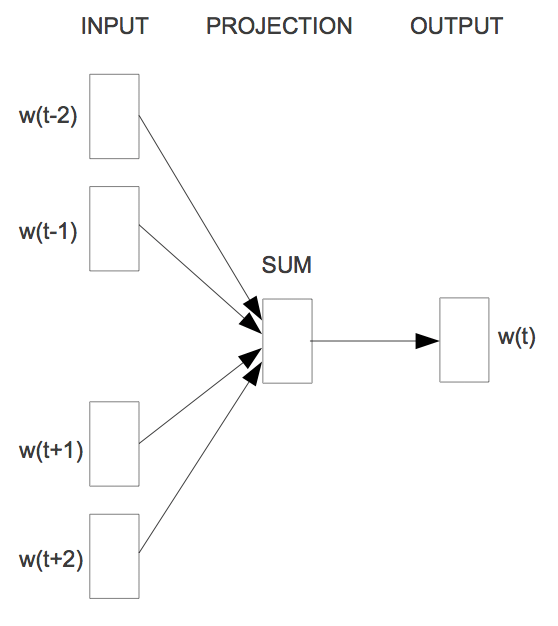
  对于其模型而言，去掉了之前的Hidden Layer，增加了一个Projection Layer，之前是将所有向量拼接，而现在是将所有向量求和，减少了参数数目，大体的模型如下。

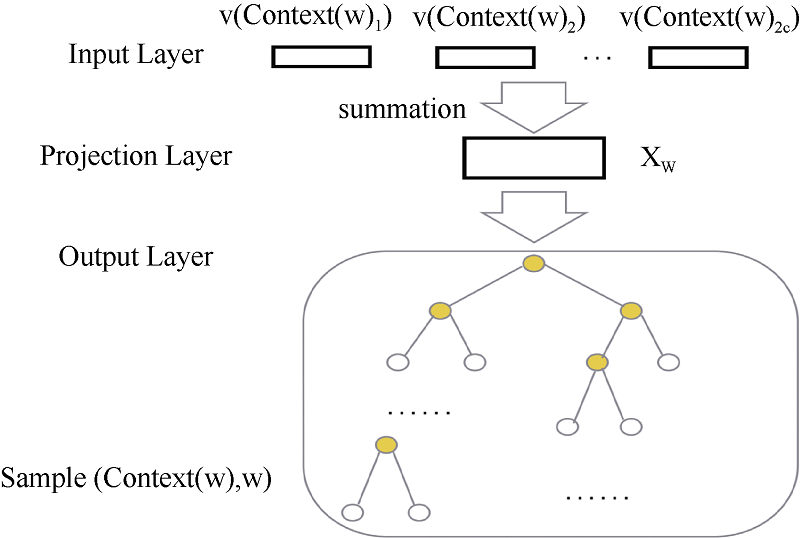
• 输入层：$Context(w)$中2c个词的词向量。

• 投影层：输入的2c个词向量的累加，即$x_w = \displaystyle\sum_{i=1}^{2c}v(Context(w)_i)$。

• 输出层：是一棵以词频为权值的Huffman树，这其中每一个叶子节点都代表一个单词，每一个非叶子节点都可以视作一次二分类。

  如果我们将其看作多分类问题，由于词典非常庞大，softmax的计算时间会线性增长，开销太大。所以此处采用了一种叫hierarchical softmax的技术，很形象，将输出层变成了一棵二叉树，并对每个非叶子节点做logisitic回归，目标节点就是我们训练集中的真实的词，也就是从根节点到目标层对应的路径就是每次分类正确的结果。

  如何更新参数呢。对于单个非叶子节点而言，它被分为正类的概率是$\sigma(x_w^T\theta)= \displaystyle\frac{1}{1+e^{-x_w^T\theta}}$，分为负类的概率是$1-\sigma(x_w^T\theta)$。在word2vec的源码中，将哈夫曼编码为1（向左走）视为负类，0（向右走）视为正类。不妨设到目标叶子节点共有s层，其中从根节点到目标叶子节点之前的非叶子节点的参数为$\theta_1,\theta_2,\dots,\theta_{s-1}$，目标叶子节点的哈夫曼编码为$d_2,d_3,\dots,d_s$，则可以得到

$$p(d_j|x_w, \theta_{j-1})= \begin{cases} \sigma(x_w^T\theta_{j-1}), &d_j = 0;\\ 1-\sigma(x_w^T\theta_{j-1}), &d_j = 1, \end{cases}$$

写成整体表达式就是

$$p(d_j|x_w, \theta_{j-1}) = \left[\sigma(x_w^T\theta_{j-1})\right]^{1-d_j}\cdot\left[1-\sigma(x_w^T\theta_{j-1})\right]^{d_j}$$

以上是一个结点的情况，如要求$p(w|Context(w))$将每个节点概率相乘即可，也就是

$$p(w|Context(w))=\displaystyle\prod_{j=2}^{s}p(d_j|x_w, \theta_{j-1})$$

为了方便计算取对数，表示如下

$$\begin{align} L &= \displaystyle\sum_{w\in C}log\prod_{j=2}^{s_w}\left[p(d_j^w|x_w, \theta_{j-1}^w)\right] \\ &=\displaystyle\sum_{w \in C}\sum_{j=2}^{s_w}\left\{(1-d_j^w)log\left[\sigma(x_w^T\theta_{j-1}^w)\right]+d_j^wlog\left[1-\sigma(x_w^T\theta_{j-1}^w)\right]\right\} \end{align}$$

以上就是CBOW的目标函数，注意d和$\theta$都有上标的原因是表示他们是$w$相关的。由于我们的目标是将这个函数最大化，所以要用Gradient Ascent。对于我们的整个模型，需要训练的参数有$\theta_{j-1}^w,x_w$，分别对他们求梯度，由于是加法，又由于对一个固定的w和j，对$\theta_j^w$求偏导有贡献的项仅仅有花括号中的w和j相同的对应项，而对$x_w$而言有贡献的是$j\in[2, s_w]$部分的花括号中的内容的偏导和，为方便计算，将花括号中的内容记作T。

$$\begin{align} \frac{\partial T}{\partial\theta_{j-1}^w} &= \displaystyle\frac{\partial}{\partial\theta_{j-1}^w}\left\{(1-d_j^w)log\left[\sigma(x_w^T\theta_{j-1}^w)\right]+d_j^wlog\left[1-\sigma(x_w^T\theta_{j-1}^w)\right]\right\}\\ &=(1-d_j^w)(1-\sigma(x_w^T\theta_{j-1}^w))\displaystyle\frac{\partial x_w^T\theta_{j-1}^w}{\partial\theta_{j-1}^w} + d_j^w\cdot(-\sigma(x_w^T\theta_{j-1}^w))\displaystyle\frac{\partial x_w^T\theta_{j-1}^w}{\partial\theta_{j-1}^w}\\ &=(1-d_j^w)(1-\sigma(x_w^T\theta_{j-1}^w))x_w - d_j^w\sigma(x_w^T\theta_{j-1}^w)x_w\ \ \ \ (矩阵求导分母布局)\\ &=\left[(1-d_j^w-\sigma(x_w^T\theta_{j-1}^w)\right]x_w \end{align}$$

对于$\displaystyle\frac{\partial T}{\partial x_w}$，与上面的过程类似，可以得到

$$\displaystyle\frac{\partial T}{\partial x_w} =\left[(1-d_j^w-\sigma(x_w^T\theta_{j-1}^w)\right]\theta_{j-1}^w$$

显然，对于参数$\theta_{j-1}^w$的更新，很容易，只需要

$$\theta_{j-1}^w\leftarrow\theta_{j-1}^w+\eta\left[1-d_j^w-\sigma(x_w^T\theta_{j-1}^w)\right]x_w$$

而对于$x_w$，它是通过v(w)累加来的，所以我们真正应该更新的是v(w)，word2vec的做法如下

$$v(w)\leftarrow v(w) + \eta\displaystyle\sum_{j=2}^{s_w}\left[1-d_j^w-\sigma(x_w^T\theta_{j-1}^w)\right]\theta_{j-1}^w,\ \ \ \ w\in Context(w)$$

这样做当然有一定道理，因为我们仅仅求出了他们的一个集体梯度，所以要将这个集体梯度反馈到每一个个体上。

综上对于一个训练样本$(Context(w), w)$，CBOW伪代码如下

$$e\leftarrow0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ x_w\leftarrow\displaystyle\sum_{w\in Context(w)} v(w)\\ for \ j \leftarrow2\ to\ s_w\ do\\ \ \ q \leftarrow \sigma(x_w^T\theta_{j-1}^w)\\ \ \ \ \ \ \ \ \ g \leftarrow\eta(1-d_j^w-q)\\ \ \ e\leftarrow e + g\theta_{j-1}^w\\ \ \ \ \ \ \ \ \ \ \theta_{j-1}^w\leftarrow \theta_{j-1}^w+gx_w\\ end\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ for \ u \in Context(w) do\\ \ \ \ \ \ \ v(u) \leftarrow v(u) + e$$

Skip-gram

  与CBOW相反，这个模型要解决的问题是在已知词$w_t$的情况下，预测词$w_{t-2}, w_{t-1},w_{t+1},w_{t+2}$。也就是要计算$P(Context(w_t)|w_t)$，如下图所示：

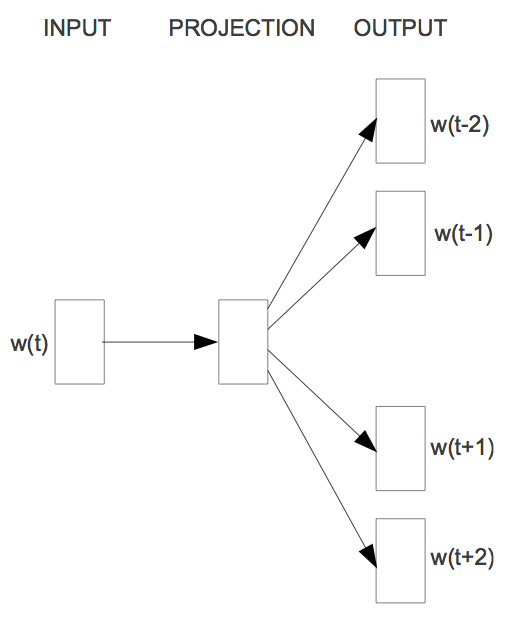
  对于其模型，与CBOW模型类似，为了与其对比，保留了projection layer，如下：

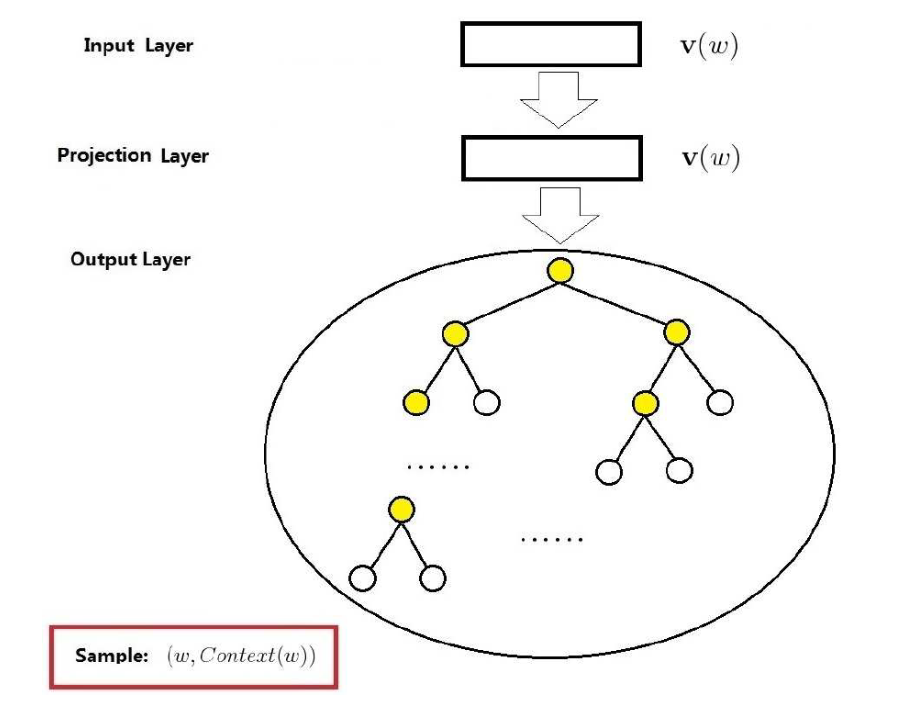
• 输入层：词向量$v(w)$

• 投影层：为了与CBOW保持类似保留的，无实际作用。

• 输出层：一棵Huffman树。与CBOW类似，也是为了利用Hierarchical softmax，所输出的一棵以单词为叶子节点，非叶子节点作为二分类的单元的哈夫曼树。

如何表示$P(Context(w)|w)$呢，可以将其拆解如下：

$$p(Context(w)|w) = \displaystyle\prod_{u \in Context(w)}p(u|w)$$

此处的$p(u|w)$可以借助CBOW的表示方式，表示为：

$$p(u|w) = \displaystyle\prod_{j=2}^{s}p(d_j|v_w, \theta_{j-1})$$

此处的$\theta,d_j$在总体表示中，同样是与语料中的$u$是相关的，将p写作二分类的形式后再取对数（与CBOW中操作相似），得到总体的目标函数

$$\begin{align} L&= \displaystyle\sum_{w\in C}log\prod_{u\in Context(w)}\prod_{j=2}^{s_u}\left[p(d_j^u|v_w,\theta_{j-1}^u)\right]\\ &= \displaystyle\sum_{w \in C}\sum_{u\in Context(w)}\sum_{j=2}^{s_u} \left\{(1-d_j^u)log\left[\sigma(v_w^T\theta_{j-1}^u)\right]+d_j^ulog\left[1-\sigma(v_w^T\theta_{j-1}^u)\right]\right\} \end{align}$$

出于与CBOW中同样的考虑，可将后面花括号中的内容记为T，与CBOW中推导过程完全相同，得到下面的结果：

$$\displaystyle\frac{\partial T}{\partial\theta_{j-1}^u} =\left[(1-d_j^u-\sigma(v_w^T\theta_{j-1}^u)\right]v_w$$ $$\displaystyle\frac{\partial T}{\partial v_w}=\left[(1-d_j^u-\sigma(v_w^T\theta_{j-1}^u)\right]\theta_{j-1}^u$$

参数更新也是类似的（此处也是要求目标函数最大值）

$$\theta_{j-1}^u \leftarrow \theta_{j-1}^u + \eta\left[(1-d_j^u-\sigma(v_w^T\theta_{j-1}^u)\right]v_w$$ $$v_w\leftarrow v_w + \eta\displaystyle\sum_{u\in Context(w)}\sum_{j=2}^{s_u}\left[(1-d_j^u-\sigma(v_w^T\theta_{j-1}^u)\right]\theta_{j-1}^u$$

综上对于一个训练样本$(w, Context(w))$，Skip-gram伪代码如下

$$e\leftarrow 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ for\ u \in Context(w)\ do \\ for \ j \leftarrow2\ to\ s_u\ do\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ q \leftarrow \sigma\left[v(w)^T\theta_{j-1}^u\right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ g \leftarrow\eta(1-d_j^u-q)\\ \ \ \ \ \ \ \ \ e\leftarrow e + g\theta_{j-1}^u\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \theta_{j-1}^u\leftarrow \theta_{j-1}^u+gv(w)\\ end\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ end\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ v(w) \leftarrow v(w)+e\ \ \ \ \ \ \ \ \ \ \ \$$

但是在word2vec中，真实的做法是每处理一个$Context(w)$中的词，就进行一次更新，也就是如下的步骤：

$$for\ u \in Context(w)\ do \\ e\leftarrow 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ for \ j \leftarrow2\ to\ s_u\ do\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ q \leftarrow \sigma\left[v(w)^T\theta_{j-1}^u\right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ g \leftarrow\eta(1-d_j^u-q)\\ \ \ \ \ \ \ \ \ e\leftarrow e + g\theta_{j-1}^u\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \theta_{j-1}^u\leftarrow \theta_{j-1}^u+gv(w)\\ end\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ v(w) \leftarrow v(w)+e\ \ \ \\ end\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\$$

  以上两种就是基于Hierarchical softmax的CBOW和Skip-gram模型，还有基于Negative Sampling的两种模型，在这里暂且不提。如果想得知更多细节，可以在源码中获得，我个人只看过java版本的，没看过纯C版本的，尽管语言不同，但我想在一些处理细节上是相同的。